Главная  Статьи Статьи  Математика Математика  Классические задачи исследования операций Классические задачи исследования операций
Классические задачи исследования операций
Рассмотрим некоторые классические задачи, традиционно относящиеся к
проблематике исследования операций.
Задача диеты (или задача о рационе) — задача линейного программирования,
состоящая в определении такого рациона, который удовлетворял бы потребности
человека или животного в питательных веществах при минимальной общей стоимости
используемых продуктов. Это частный (наиболее распространенный) случай более
общей задачи об оптимальном составе смеси.
Задача составления оптимального рациона для человека сложна, так как
приходится учитывать много дополнительных, не всегда формализуемых факторов —
вкусовые привязанности, разнообразие блюд и т. д. Однако в животноводстве
определение рационов для скота с помощью задачи линейного программирования
сегодня не просто реально, но и необходимо. Опыт показывает, что кормление скота
рационами, рассчитанными по этому методу, дает существенную экономию. Например,
в США ими пользуются многие фермеры. Это не означает, разумеется, что каждый сам
решает задачу линейного программирования: в разных районах страны издаются
справочники рационов кормления, учитывающие местные особенности и возможности,
породы скота и т. д.
Модель задачи можно записать так (см. также рис. 2.5 и примеры 2.4, 2.5):
найти минимум суточных затрат на продукты питания
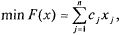
где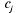 —
цена; —
цена;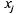 —
количество продукта под номером —
количество продукта под номером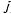 ; ;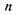 — количество таких продуктов при
условии — количество таких продуктов при
условии
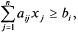
т. е. в рационе должно содержаться не менее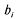 питательного вещества с
номером питательного вещества с
номером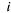 ; ;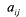 — количество — количество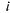 -го вещества в
единице -го вещества в
единице 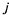 -го
продукта; кроме того, должно выполняться условие неотрицательности: -го
продукта; кроме того, должно выполняться условие неотрицательности:
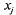 > 0. > 0.
Задача замены заключается в прогнозе затрат, связанных с обновлением
оборудования, и в выработке наиболее экономичной стратегии проведения этой
работы. Выработан ряд методов, позволяющих решать задачи замены двух типов:
а) производительность оборудования падает в процессе эксплуатации
(вследствие износа), и оно устаревает морально в результате появления новых,
более совершенных машин;
б) оборудование не устаревает, но в некоторый момент выбывает из строя
(например, электролампочки).
В первом случае сравниваются затраты на приобретение нового оборудования с
издержками эксплуатации действующего и находится оптимальный момент замены. Для
решения некоторых из таких задач применимы методы динамического
программирования.
Во втором случае определяют, какие именно единицы надо заменять и как часто
производить замену, чтобы минимизировать общие затраты, связанные как с покупкой
нового оборудования, так и с ущербом, который наносит неисправное оборудование
до его замены. В этих задачах широко используются м а -тематико-статистические
методы, так как выход из строя оборудования всегда имеет нерегулярный,
вероятностный характер.
Задача о коммивояжере состоит в отыскании наилучшего маршрута для
коммивояжера (бродячего торговца), который должен объехать все порученные ему
города и вернуться назад за кратчайший срок или с наименьшими затратами на
проезд. Это — одна из типичных задач, решаемых методом динамического
программирования. О сложности ее говорит такой факт: если городов — 4, то число
возможных маршрутов равно 6, а уже при 11 городах существует более 3,5 млн
допустимых маршрутов. В общем случае, когда число городов п, количество
маршрутов равно (n - 1)!, т. е. «(n - 1) факториал». Задача заключается в поиске
сокращенных способов расчета, позволяющих отказаться от сплошного перебора
возможных маршрутов.
Алгоритмы, позволяющие решать на электронных вычислительных машинах
задачу о коммивояжере, используются не только при выборе маршрутов
автотранспорта при кольцевой доставке товаров (например, в торговую
сеть), но и при решении таких задач, которые на первый взгляд никакого
отношения к задаче коммивояжера не имеют, например в планировании
производства на конвейерах, выпускающих машины различных моделей. На
ЭВМ с помощью таких алгоритмов рассчитывают оптимальные партии,
позволяющие выпускать заданный объем продукции с минимумом затрат на
переналадку конвейера.
Распределительные задачи — класс экономико-математических задач, связанных с
распределением ресурсов по работам, которые необходимо выполнить. Если ресурсов
достаточно, чтобы каждую работу выполнить наиболее эффективно, задача не
возникает. В обратном случае переброска, передача ресурсов с одной работы на
другую приводит к изменению общей эффективности всех работ, вместе взятых.
Поэтому распределительная задача заключается в отыскании наилучшего
распределения ресурсов, при котором либо максимизируется общий доход или
результат, выраженный в какой-либо другой форме, либо минимизируются
затраты.
Такие задачи чаще всего приводятся к линейному виду (иногда искусственно за
счет упрощений) и решаются методом линейного программирования. Если через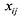 обозначить объем
ресурса обозначить объем
ресурса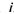 ,
выделенного на работу ,
выделенного на работу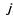 , то математическая формулировка распределительной задачи такова: найти
минимум или максимум целевой функции (минимум затрат , то математическая формулировка распределительной задачи такова: найти
минимум или максимум целевой функции (минимум затрат
min 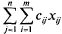 или
максимум эффекта max или
максимум эффекта max ![]() alt="" src="/pic/matm/tmp178-17.jpg"
width=74>при ограничениях по объему ресурсов и потребности в них. При этом различаются два
вида таких задач:
alt="" src="/pic/matm/tmp178-17.jpg"
width=74>при ограничениях по объему ресурсов и потребности в них. При этом различаются два
вида таких задач:
а) сбалансированная (закрытая), если общий объем ресурсов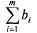 равен общей потребности в
них равен общей потребности в
них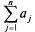 ; ;
б) несбалансированная (открытая), когда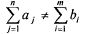 и требуется не только
распределить ресурсы по работам (потребителям), но также решить, какие работы не
следует выполнять (т. е. каких потребителей не удовлетворять), если ресурсы
меньше потребностей, либо какие ресурсы не использовать — в противоположном
случае. и требуется не только
распределить ресурсы по работам (потребителям), но также решить, какие работы не
следует выполнять (т. е. каких потребителей не удовлетворять), если ресурсы
меньше потребностей, либо какие ресурсы не использовать — в противоположном
случае.
К распределительным задачам относятся такие широко распространенные задачи,
как транспортная задача, задача о назначениях и многие другие. Задачи распределения могут решаться в статической
(однократной) и в динамической постановке. В последнем случае часто применяют
методы стохастического программирования (в которых принятие решений основано на
вероятностных оценках будущих значений параметров).
Задача о назначениях — вид задачи линейного программирования, с помощью
которой решаются вопросы типа: как распределить рабочих по станкам, чтобы общая
выработка была наибольшей или затраты на заработную плату наименьшими (поскольку
для каждой комбинации «рабочий—станок» характерна своя производительность
труда), как наилучшим образом распределить экипажи самолетов, как назначить
людей на различные должности (отсюда и название задачи) и т. д.
Математически такие задачи — частный случай распределительных задач с той
особенностью, что в них объемы наличных и требующихся для выполнения каждой
работы ресурсов равны единице, т. е.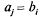 = =1, и = =1, и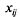 =1, если работник =1, если работник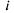 назначен на работу назначен на работу 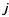 , или
нулю в остальных случаях. Иначе говоря, для выполнения каждой работы расходуется
только один вид ресурса, а каждый ресурс может быть использован на одной работе:
ресурсы неделимы между работами, а работы — между ресурсами. Исходные данные
группируются в таблице, которая называется «матрицей оценок», результаты — в
«матрице назначений». , или
нулю в остальных случаях. Иначе говоря, для выполнения каждой работы расходуется
только один вид ресурса, а каждый ресурс может быть использован на одной работе:
ресурсы неделимы между работами, а работы — между ресурсами. Исходные данные
группируются в таблице, которая называется «матрицей оценок», результаты — в
«матрице назначений».
Количество возможных вариантов назначений равно факториалу числа работ и
ресурсов и огромно даже в небольшой задаче. Поэтому для нахождения оптимального
варианта применяют специальные алгоритмы. Среди них особенно эффективен при
решении задачи вручную так называемый «венгерский метод».
Задача о раскрое — частный случай задач о комплексном использовании сырья,
обычно сводящихся к методу линейного программирования. Выработанный математиками
метод решения задачи о раскрое помогает с наименьшими отходами использовать
прутки и листы металла, листы стекла, картона и других материалов при раскрое их
на заданное количество деталей различных размеров.
Постановку задачи в общем виде можно сформулировать так: требуется найти
минимум линейной формы, выражающей число израсходованных листов материала (листов и т. п.) по всем j-м способам их
раскроя:
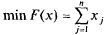
при условии, что переменные удовлетворяют ограничению
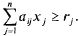
Это означает, что соблюдена комплектность: все необходимые заготовки сделаны
в достаточном количестве,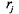 ( (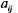 — число заготовок i-го типа при
j-м способе раскроя; — число заготовок i-го типа при
j-м способе раскроя;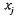 — число листов, раскроенных j-м способом). Наконец, принимается условие
неотрицательности: — число листов, раскроенных j-м способом). Наконец, принимается условие
неотрицательности: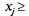 0, т. е. число листов не может быть отрицательно. 0, т. е. число листов не может быть отрицательно.
Способы постановки и решения таких задач хорошо отработаны и их можно
применять на любом предприятии. При правильной постановке задачи применение
метода линейного программирования гарантирует сокращение отходов до минимально
возможного. Часто на предприятиях отходы сокращаются в несколько раз.
Задачи поиска — класс задач, состоящих в отыскании наилучшего способа
получения такой информации, которая однозначно определила бы решение. Критерием
в такой задаче является минимум затрат двух видов: стоимости получения
информации и цены ошибки, обусловленной ее использованием. В первом случае речь
идет о стоимости выборки, планирование которой сводится к определению способа
выбора наблюдений или выбора наблюдаемых объектов, во втором случае — об ошибках
двух родов: ошибке выборки (обнаружение того, что в действительности отсутствует
— «ложная тревога») и ошибке наблюдения (пропуск того, что на самом деле имеет
место — «пропуск цели»).
Задачи согласования — класс задач, связанных с согласованием совокупности
отдельных работ и частных операций во времени для получения оптимального общего
результата. Это обычно задачи сетевого планирования и управления.
Задачи упорядочения — класс задач, в которых производится выбор дисциплины
обслуживания. Таким образом, они как бы противоположны задачам теории массового
обслуживания, в которых дисциплина (т. е. порядок выполнения требований) задана.
Выбор порядка обслуживания называется упорядочением. Наиболее распространены
среди задач (моделей) упорядочения задачи теории расписаний. К ним относятся
также методы ситуационного управления и некоторые другие.
Задачи теории расписаний — один из видов задач исследования операций,
объединяемых в классе задач упорядочения. Теорией расписаний называется здесь
совокупность моделей календарного планирования и разработанных для их решения
методов дискретного программирования.
Сложность таких задач можно проиллюстрировать примером: требуется
спланировать изготовление четырех изделий, каждое из которых проходит обработку
на каждом из пяти станков. Существует (4!)5 или почти 7962 тыс. различных
вариантов обработки (последовательностей); некоторые из них к тому же надо
как-то отсеять, поскольку определенные операции следует выполнять в заданном
порядке. На практике, разумеется, задачи намного сложнее.
Проще других решаются так называемые задачи одного станка: поиск наилучшей
последовательности обработки на нем некоторого множества деталей (наилучшей с
точки зрения минимума затрат на пролеживание деталей до обработки и после нее,
минимума времени задержки в выдаче деталей по сравнению с установленным сроком,
минимального объема незавершенного производства и т. п.).
Существует также ряд моделей планирования работы производственного участка
(методическую основу для них дает модель Джонсона для п деталей и двух станков,
но она представляет лишь теоретический интерес и малоприменима на практике).
Наконец, теория расписаний содержит методы составления календарных планов работы
предприятий. Обычно задача ставится таким образом: составить план изготовления
всех изделий, в котором не нарушались бы технологические ограничения,
ограничения по мощности оборудования, а также сроки запуска и выпуска. Такие
задачи решаются обычно приближенными методами, в том числе методом Монте-Карло и
др. В описанных условиях большое значение имеют способы сокращения размерности задач. Теория
расписаний — теоретическая база оптимального календарного планирования.
Использует ряд методов линейного программирования, дискретного программирования,
методы ветвей и границ, сетевого планирования и управления и др. Модели теории
расписаний позволяют, например, решать такие задачи, как определение оптимальной
последовательности обработки деталей на станках, планирование работы
производственного участка, составление программы-«диспетчера» для управления
работой электронной вычислительной машины в мультипрограммном режиме.
Задача о размещении складов — одна из задач, обычно решаемая методом
нелинейного программирования (но при некоторых условиях она может сводиться и к
обычной транспортной задаче линейного
программирования). Заключается в
минимизации общей суммы транспортных и складских расходов при следующих
ограничениях: с каждого завода должна быть отгружена вся продукция, емкость
любого склада не должна быть превышена, потребности всех покупателей должны быть
удовлетворены. По существу дело сводится к отысканию трехзвенных комбинаций
предприятие — склад — потребитель, в совокупности обеспечивающих минимум
расходов.
Управление запасами — комплекс моделей и методов, предназначенных для
оптимизации запасов, т. е. ресурсов, находящихся на хранении и предназначенных
для удовлетворения спроса на эти ресурсы. Термины ресурсы и запасы здесь
понимаются обобщенно: можно говорить о запасах конечной продукции, о запасах
полуфабрикатов (тогда соответствующая задача будет задачей об оптимизации
незавершенного производства), о запасах сырья, природных и трудовых ресурсов,
денежных средств и т. д. Роль производства сводится здесь к пополнению уровня
запасов по мере возникновения потребности в них. Другим источником
удовлетворения заявок на ресурсы является склад, собственно запас.
В качестве целевой функции в задачах управления запасами выступают суммарные
затраты на содержание запасов, на складские операции, потери от порчи при
хранении и моральное старение, потери от дефицита и штрафы и т. д. Естественно,
что отслеживается минимум этой функции. Управляемыми переменными в таких задачах
являются объем запасов, частота и сроки их пополнения (путем производства,
закупки и т. д.), степень готовности продукции, хранящейся в виде запасов и др.
Задачи бывают статические (когда принимается разовое решение об уровне запаса на
определенный период) и динамические, или многошаговые, когда принимаются
последовательные решения или корректируется ранее принятое решение с учетом
происходящих изменений. Упрощенным примером задач управления запасами может
служить задача об оптимальной партии.
Теория игр — раздел, изучающий математические модели конфликтных ситуаций (т.
е. ситуаций, при которых интересы участников либо противоположны и тогда эти
модели называются антагонистическими играми, либо не совпадают, хотя и не
противоположны, и тогда речь идет об играх с непротивоположными интересами.)
Основоположники теории Дж. фон Нейман и О. Моргенштерн попытались математически
описать явления конкуренции как некую «игру». В наиболее простом случае речь
идет о противоборстве только двух противников, например двух конкурентов,
борющихся за рынок сбыта. В более сложных случаях в игре участвуют многие,
причем они могут вступать между собой в постоянные или временные коалиции,
союзы. Игра двух лиц называется парной; когда в ней участвуют п игроков, это
игра п лиц, в случае образования коалиций игра называется коалиционной.
Суть игры в том, что каждый из участников принимает такие решения (т. е.
выбирает стратегии действий), которые, как он полагает, обеспечивают ему
наибольший выигрыш или наименьший проигрыш, причем этому участнику игры ясно,
что результат зависит не только от него, но и от действий партнера (или
партнеров), иными словами, он принимает решения в условиях неопределенности. Эти
решения отражаются в таблице, которая называется платежной матрицей. Часто
обнаруживается такая точка (седловая),в которой достигается равновесие,
приемлемое для партнеров.
Чисто математическая и потому весьма абстрактная теория игр, разумеется,
далеко не полно отражает сложные процессы, происходящие в экономике, однако
теоретическое и практическое ее значение намного шире.
Принципиальным достоинством теории игр считают то, что она расширяет
общепринятое понятие оптимальности, включая в него такие важные элементы, как,
например, компромиссное решение, устраивающее разные стороны в подобном споре
(игре). Кроме того, математические приемы теории игр могут применяться для
решения многочисленных практических экономических задач на промышленных
предприятиях. Например, для выбора оптимальных решений в области повышения
качества продукции или определения запасов. «Противоборство» здесь происходит в
первом случае между стремлением выпустить больше продукции (затратить на нее
меньше труда) и сделать ее лучше, т. е. затратить больше труда, во втором случае
— между желанием запасти ресурсов побольше, чтобы быть застрахованным от
случайностей, и запасти поменьше, чтобы не замораживать средства.
Следует отметить, что подобные задачи решаются и другими способами. И это не
случайно — многие задачи теории игр могут быть сведены, например, к задачам
линейного программирования, и наоборот.
Задачи массового обслуживания — класс задач, заключающихся в нахождении
оптимальных параметров систем массового обслуживания.
Слова оптимальные параметры здесь можно понимать двояко: как характеристики
структуры системы (выбор числа каналов обслуживания, их последовательности,
пропускной способности) и как характеристики функционирования системы
(формирование входящего потока, выбор наилучшей дисциплины обслуживания и т.
п.).
Важнейшими частными критериями качества систем массового обслуживания
являются:
• вероятность удовлетворения заявки (требования) или задержки в
обслуживании;
• математическое ожидание числа удовлетворенных (задержанных) заявок за
фиксированное время;
• математическое ожидание числа занятых каналов обслуживания;
• математическое ожидание длины очереди.
В целом же можно считать, что наиболее важным критерием оптимальности в таких
задачах должны быть средние суммарные потери от ожидания требований, с одной стороны, и простоя каналов
обслуживания — с другой.
Аналитическим путем решаются лишь наиболее простые задачи, на практике все
шире применяются методы статистического моделирования, особенно метод
Монте-Карло.
Нет комментариев.
Оставлять комментарии могут только зарегистрированные пользователи
Обсудить в форуме. (0 комментариев)
|
