| Главная |
| Лекции |
| Практика |
| Лабораторные |
| Словарь |
| Формулы |
| Литература |
|
|
Модели управления запасами
1. Зависимый и независимый спрос. Предмет теории управления запасами.
2. Основные стратегии управления запасами.
3. Модификации основных стратегий управления запасами.
4. Целевые функции моделей управления запасами.
5. Типы моделей управления запасами.
6. Простейшие модели управления запасами.
6.1 Однопродуктовая статическая модель.
6.2 Однопродуктовая статическая модель, допускающая дефицит
6.3 Модель с постепенным пополнением запасов.
6.4 Модель с постепенным пополнением запасов, допускающая дефицит
7. Вероятностные модели управления запасами.
7.1 Модель с фиксированным размером заказа и уровень обслуживания.
7.2 Модель с фиксированной периодичностью заказа и уровень обслуживания.
8. Специальные модели управления запасами.
8.1 Модель, учитывающая количественные скидки.
Модель управления запасами простейшего типа характеризуется тремя свойствами:
постоянным во времени спросом;
мгновенным пополнением запаса;
отсутствием дефицита.
В
этом случае модель с фиксированным размером заказа и модель с
фиксированной периодичностью ведут себя совершенно одинаково, поскольку
интенсивность спроса и продолжительность заготовительного периода не
изменяются. На практике такой модели могут соответствовать следующие
ситуации: использование осветительных ламп в здании; использование
крупной фирмой канцелярских товаров: бумаги, блокнотов, карандашей и
т.д., потребление основных продуктов питания. График движения запаса на складе для подобной ситуации представлен на рисунке 4.8. На рисунке обозначены:
q - размер партии;
Z ср = q/2 - средний уровень запаса;
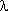 - тангенс соответствующего угла, интенсивность спроса (количество продукции, потребляемой в единицу времени);
S – «точка заказа»;
 – продолжительность заготовительного периода;
l - продолжительность цикла заказа (планируемого периода).
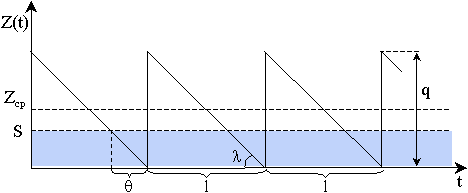
Рисунок 4.8 – Движение запаса в однопродуктовой статической модели
Для такой модели размер запаса в определеный момент времени может быть рассчитан по формуле:
Z(t) = Z(0) - 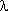 t + W(t), t + W(t),
|
(4.4)
|
где W(t) - суммарное поступление продукта за период [0,t].
Величина суммарных поступлений определяется из соотношения:
где n(t) - полное число поставок за период [0,t].
При этом l = 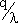 , т.е. уровень запаса достигнет нуля, спустя 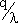 единиц времени после получения заказа размером q.
Полное число поставок:
n(t) = 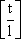 = = 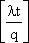 , ,
|
(4.6)
|
где [ ] - целая часть числа.
Из соотношений (4.4), (4.5) и (4.6) получим:
Z(t) = Z(0) - 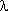 t + q∙ t + q∙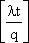 . .
|
(4.7)
|
Уравнение (4.7) полностью описывает рассматриваемую систему хранения запаса.
Оптимизация заключается в выборе наиболее экономичного размера партии q. Утверждение иллюстрирует рисунок 4.9.
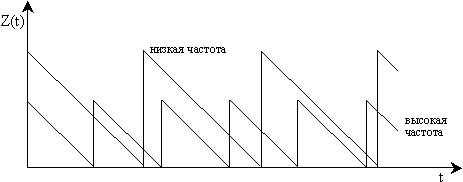
Рисунок 4.9 – Экономический смысл оптимального размера партии
Чем меньше q, тем чаще нужно размещать новые заказы. Однако при этом средний уровень запаса будет уменьшаться.
С другой стороны, с увеличением q уровень запаса повышается, но заказы размещаются реже.
Так
как затраты зависят от частоты заказов и объема хранимого запаса, то
величина q должна определяться из условия обеспечения
сбалансированности между двумя видами затрат. Итак, с 0, как и прежде, - затраты на оформление
заказа, имеющие место всякий раз при его размещении; b - затраты на
хранение единицы продукции в единицу времени; с 1 - закупочная цена единицы продукта; d(t) - общий объем потребленной продукции за период [0,t].
Выразим суммарные затраты V(t) за период времени [0,t] и зададимся целью отыскать минимум этих затрат:
|
V(t) = c0n(t) + b∙Zср∙t + c1d(t) → min.
|
|
Используя соотношения (4.6) и (4.7) и
переходя к затратам в единицу времени (для этого разделим предыдущее
выражение на t), получим:
Заметим, что требованием о целой части в выражении (4.6) нам пришлось пренебречь, чтобы получить дифференцируемую функцию.
Далее найдем производную функции по q и приравняем ее нулю:
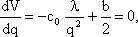
|
|
откуда найдем q:
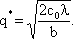
|
(4.8)
|
Заметим, что вторая производная в точке q * строго положительна, что говорит о том, что найден именно минимум функции.
Соотношение (4.8) принято называть формулой экономичного размера заказа Уилсона. Формула Уилсона занимает центральное место во всей теории управления запасами.
Таким образом, оптимальная стратегия модели предусматривает заказ q * единиц продукта через каждые l * = 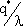 единиц времени.
Стратегия
размещения заказов в приведенной модели должна определять также "точку
заказа". Можно показать, что "точка заказа" для данного случая
определяется как:
S* = 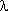  . .
|
(4.9)
|
При использовании формул (4.8) и (4.9) необходимо контролировать, чтобы интенсивность спроса 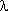 и стоимость хранения b были отнесены к одному и тому же промежутку времени, например, к году, месяцу или дню. В отношении оптимального объема партии q * необходимо сделать следующее замечание.
Стоимость
хранения и стоимость заказа, а также предполагаемый спрос, - все это по
своей сути ориентировочные показатели, их невозможно точно рассчитать.
Иногда стоимость хранение не рассчитывается, а просто устанавливается, исходя из каких-то разумных соображений. Соответственно, экономичный объем заказа нужно считать приблизительным, а не точным показателем. Так, вполне допустимо округление
полученной величины. Расчеты с точностью до нескольких десятичных
знаков могут создать ложное впечатление о точности данного показателя.
Возникает вопрос: в какой степени приемлем такой "приблизительный"
объем партии с точки зрения минимальных расходов? Ответ состоит в том,
что кривая издержек в районе точки q* относительно пологая,
особенно вправо от данной точки (см. рисунок 4.10). Следовательно,
показатель экономичного объема партии можно считать достаточно
устойчивым.
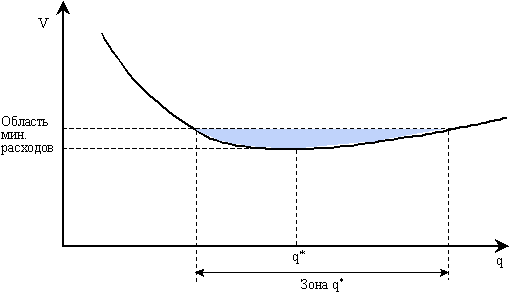
Рисунок 4.10 – Зона оптимального размера партии
В
рассмотренной выше простейшей модели дефицит продукции не допускается.
В общем случае, когда потери от дефицита сопоставимы с расходами по
содержанию запасов, дефицит допустим. График движения запаса для такой ситуации приведен на рисунке 4.11, где 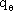 обозначает количество продукции, потребляемой в течение заготовительного периода. 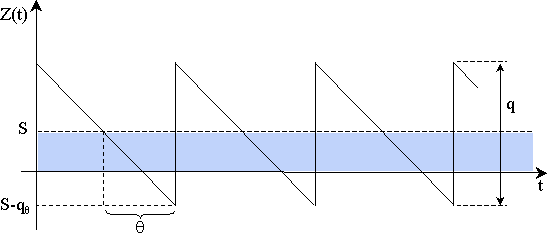
Рисунок 4.11 – Движение запаса в однопродуктовой статической модели, допускающей дефицит
Не производя подробного вывода формул, скажем следующее.
В случае, когда вид минимизируемой функции определяется посредством соотношений (4.1) - (4.3), оптимальные значения параметров q * и S * имеют следующий вид:
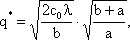
|
(4.10)
|
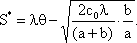
|
(4.11)
|
Нетрудно заметить, что при больших издержках от неудовлетворенного спроса, т.е. при недопустимости дефицита (a → ∞), q* и S* в формулах (4.10) и (4.11) стремятся к соответствующим значениям в формулах (4.8) и (4.9).
Простейшая
однопродуктовая статическая модель, рассмотренная нами в разделе 6.1,
обладала тремя свойствами: достоверно известный спрос, мгновенное
пополнение запаса, отсутствие дефицита. Что происходит с оптимальными параметрами модели при допущении
дефицита, мы выяснили, рассмотрев материалы раздела 6.2. А что же будет
происходить с параметрами модели в случае, когда процесс пополнения
запаса распределен во времени? Исследуем эту ситуацию.
В
некоторых случаях, например, когда предприятие одновременно является
производителем и потребителем изделий, запасы пополняются постепенно, а
не мгновенно. То есть, в данном случае одна часть производственной
системы выполняет функцию поставщика для другой части этой системы,
выступающей в роли потребителя. Если темпы производства и потребления одинаковы, то запасы
создаваться вообще не будут, поскольку весь объем выпуска сразу же
используется. В этом случае вопрос об объеме партии не рассматривается.
Чаще бывает, что темп производства превышает темп потребления. График движения запасов в такой системе будет иметь вид,
соответствующий графику, представленному на рисунке 4.12. Приведем
обозначения необходимых для дальнейшего анализа величин: q - объем производимой партии, шт.;
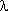 - интенсивность потребления, шт./ед. времени;
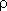 - темп производства, шт./ед. времени; соответственно, 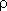 - 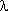 - темп прироста запасов (шт./ед. времени), на графике - тангенс соответствующего угла;
Z max - максимальный уровень запасов;
b - расходы на хранение единицы продукции в единицу времени, ед. стоимости;
c 0 - затраты на пуско-наладочные работы, ед. стоимости;
 - продолжительность пуско-наладочных работ, иначе время упреждения заказа, ед. времени. 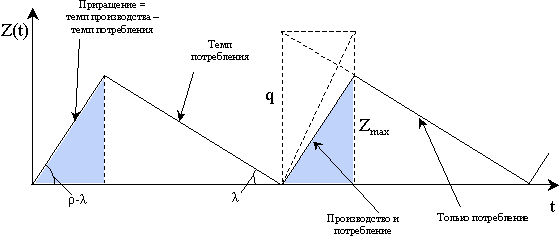
Рисунок 4.12 – Движение запасов в модели с постепенным пополнением
Из
графика видно, что изделия производятся в течение только части цикла,
потому что темп производства выше темпа потребления; потребление же
происходит на протяжении всего цикла. Во время производственной стадии
цикла создаются запасы. Их уровень равен разнице между уровнем
производства и уровнем потребления. Пока продолжается производство,
уровень запасов будет повышаться. Когда производство прекращается,
уровень запасов начинает снижаться. Следовательно, уровень запасов
будет максимальным в момент завершения производственной стадии. Когда
наличный запас будет исчерпан, производство возобновляется, и весь цикл
повторяется вновь. Когда компания сама производит изделия, то у нее нет как
таковых расходов на заказ. Однако для каждой производственной партии
существуют расходы на подготовку - это стоимость подготовки
оборудования к данному производственному процессу: наладка, замена
инструмента и т.п. По иному такие расходы называются затратами на
пуско-наладочные работы. Стоимость подготовки в данном случае
аналогична стоимости заказа, поскольку она не зависит от размера
партии. Аналогично и использование этих величин при расчетах. Перейдем к определению оптимальных параметров рассматриваемой
модели. Для этого используем прием, уже примененный нами в разделе 6.1:
составим выражение, показывающее зависимость затрат V от параметров
модели, отыщем производную и приравняем ее нулю. На этот раз включим в общие расходы всего два вида издержек:
затраты на проведение пуско-наладочных работ и затраты на хранение
продукции. Расходы, пропорциональные объему партии (компонент,
включающий величину c 1), в функцию включать не будем.
Во-первых, как мы видели выше, это слагаемое никак не влияет на
итоговые выражения для оптимальных параметров, во-вторых, в условиях,
когда предприятие одновременно является и производителем, и
потребителем продукции, такие затраты по сути не связаны с
функционированием системы хранения запасов. Итак, суммарные затраты V(t) за период времени [0,t]:
|
V(t) = c0n(t) + b∙Zср∙t → min.
|
|
Используя соотношениe (4.6) и переходя к затратам в единицу времени (для этого разделим предыдущее выражение на t), получим:
V = c0∙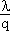 + b∙ + b∙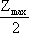 → min. → min.
|
|
Выразим Z max через q (объем
производственной партии). Это легко сделать, используя график движения
запаса, представленный на рисунке 4.12, а именно, рассматривая
некоторые треугольники и используя простейшие тригонометрические
соотношения:
откуда:
Приравняем нулю производную:
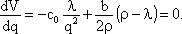
|
|
Выразим q:
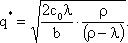
|
(4.12)
|
Выражение (4.12) используется для определения оптимального размера партии с модели с постепенным пополнением запаса.
Оптимальное значение "точки заказа" S * в этом случае, как и для однопродуктовой статической модели, находится из соотношения (4.9):
S* = 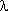  . .
|
|
"Точка заказа" в данном случае представляет собой уровень запаса, при котором следует начать пуско-наладочные работы.
В однопродуктовой статической модели (раздел 6.1) пополнение запасов
происходит мгновенно и дефицит не допускается. В разделе 6.2 мы
рассмотрели случай, когда допускается дефицит, в разделе 6.3 -
ситуацию, когда пополнение запасов происходит постепенно. Теперь рассмотрим более общий случай - дефицит допускается и запасы пополняются постепенно.
График
движения запасов в такой системе представлен на рисунке 4.13. Все
приведенные на рисунке обозначения уже использовались нами ранее.
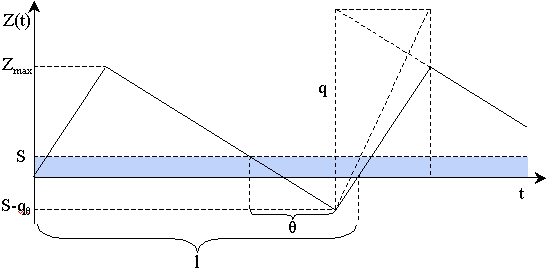
Рисунок 4.13 – Движение запасов в модели с постепенным пополнением, допускающей дефицит
Не производя вывод формул для оптимальных параметров такой модели, запишем итоговые выражения.
Оптимальный размер партии q * будет равен:
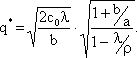
|
(4.13)
|
"Точка заказа" (критический уровень запаса, при достижении которого следует начать пуско-наладочные работы):
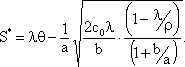
|
(4.14)
|
Оптимальная продолжительность цикла l *:
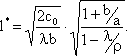
|
(4.15)
|
При данных значениях параметров достигается минимум суммарных затрат в единицу времени. Его можно рассчитать по формуле:
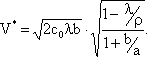
|
(4.16)
|
Итоги рассмотрения раздела 6 сведем в
таблицу 4.1, где представлены характеристики четырех изученных моделей,
а также номера формул, используемых для расчета оптимальных параметров
моделей в каждом случае.
Таблица 4.1 - Харатеристики моделей управления запасами, рассмотренных в разделе 6
Подраздел |
Характеристики модели |
Используемые соотношения |
Интенсивность
спроса |
Пополнение
запасов |
Дефицит |
6.1 |
постоянная |
мгновенное |
отсутствует |
(4.8), (4.9) |
6.2 |
постоянная |
мгновенное |
допускается |
(4.10), (4.11) |
6.3 |
постоянная |
постепенное |
отсутствует |
(4.12), (4.9) |
6.4 |
постоянная |
постепенное |
допускается |
(4.13) - (4.16) |
← Назад - К разделу - К началу страницы - Далее →
|
|





